Введение
Во многих цифровых устройствах для преобразования аналоговых сигналов используется АЦП. Часто аналоговые сигналы содержат нежелательный высокочастотный шум.
Чтобы "очистить" сигнал от этих шумов применяются аналоговые RC фильтры низких частот, которые устанавливаются после источника сигнала. Такой подход не всегда идеален и практичен. Например, для больших постоянных времени требуются большие значения R и C.
В качестве альтернативы, можно "очистить" зашумленный сигнал с помощью цифрового эквивалента аналогового RC фильтра нижних частот.
Алгоритм цифрового фильтра
По сути, программа этого цифрового фильтра состоит всего из двух строчек на Си.:
Dacc = Dacc + Din - Dout
Dout = Dacc/K
где Dout - выходное значение фильтра, Din - входное значение фильтра, K - постоянный коэффициент, который рассчитывается по формуле:
K = T x SPS
где T - это постоянная времени фильтра, SPS - частота дискретизации АЦП.
Dacc и Dout должны сохранять свои значения, после выполнения алгоритма. Если алгоритм реализовать в виде функции, то эти переменные можно просто сделать статическими.
Для 8-ми разрядных входных данных алгоритм цифрового фильтра в Си коде может выглядеть так:
#define SPS 9600UL
#define Trc 0.001f
#define K (SPS*Trc)
uint8_t Filtr(uint8_t data)
{
static uint16_t Dacc = 0;
static uint8_t Dout = 0;
uint8_t Din = data;
Dacc = Dacc + Din - Dout;
Dout = Dacc/(uint16_t)K;
return Dout;
}
Пример реализации цифрового фильтра на mega16
Для наглядности рассмотрим реальный пример использования этого алгоритма в микроконтроллере AVR atmega16. Допустим мы хотим сымитировать RC фильтр с постоянной времени 0.001 c. Схема представлена на рисунке ниже.
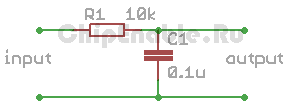
R1 = 10 кОм
C1 = 0.1 мкФ
Trc = R1*C1 = 10000 Ом * (0.1/1000000) Ф = 0.001 с
F = 1/(2*Pi*R1*C1) = 1/(6.28 * Trc) = ~50 Гц
Тактовая частота модуля АЦП в микроконтроллерах AVR зависит от его тактовой частоты и внутреннего предделителя. Допустим, наш микроконтроллер тактируется от внутреннего генератора с частотой 8 МГц, а предделитель в модуле АЦП установлен равным 64. Тогда тактовая частота модуля АЦП будет равна:
Fadc = Fcpu/Pre = 8000000/64 = 125000 Гц
Из этой частоты можно рассчитать частоту дискретизации АЦП при работе в режиме непрерывного преобразования. Она равна отношению тактовой частоты АЦП к количеству тактов, которые требуются для выполнения одного преобразования. По даташиту можно узнать, что одно преобразование выполняется за 13 тактов (если это не первое преобразование).
Fs = Fadc/n = 125000/13 = ~9600 Гц
Итак, частота дискретизации равна 9600 Гц, а постоянная времени 0.001 с. Коэффициент фильтра будет равен:
K = SPS x T = 9600 * 0.001 = 9.6 = ~ 10
Теперь все данные известны и можно написать тестовую программу для проверки алгоритма.
Я сделал эту программу очень простой. АЦП работает в режиме непрерывного преобразования. В прерывании 8-ми разрядный результат преобразования обрабатывается алгоритмом и записывается в порт C. К порту C подключен схема R-2R ЦАПа на основе резисторов, чтобы можно было сравнить полученный сигнал с сигналом от аналогового RC фильтра. Тактовая частота микроконтроллера atmega16 - 8МГц, коэффициент предделителя АЦП - 64. Тестовая схема показана на рисунке ниже. 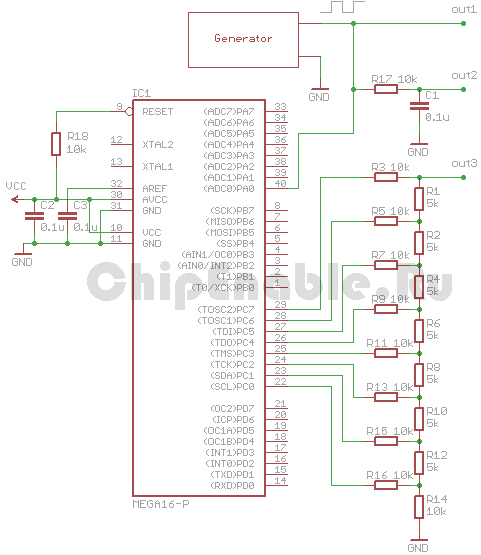
Код программы
#include <ioavr.h>
#include <intrinsics.h>
#include <stdint.h>
#define SPS 9600UL
#define Trc 0.001f
#define K (SPS*Trc)
int main( void )
{
/*инициализация АЦП*/
ADMUX = (0<<REFS1)|(1<<REFS0)|(1<<ADLAR);
ADCSRA = (1<<ADEN)|(1<<ADSC)|(1<<ADATE)|(1<<ADIE)|(1<<ADPS2)|(1<<ADPS1)|(0<<ADPS0);
/*инициализация порта*/
DDRC = 0xff;
PORTC = 0x00;
__enable_interrupt();
while(1);
return 0;
}
/*обработчик прерывания АЦП*/
#pragma vector = ADC_vect
__interrupt void Adc(void)
{
static uint16_t Dacc = 0;
static uint8_t Dout = 0;
uint8_t Din = ADCH;
Dacc = Dacc + Din - Dout;
Dout = Dacc/(uint16_t)K;
PORTC = Dout;
}
Результат моделирования
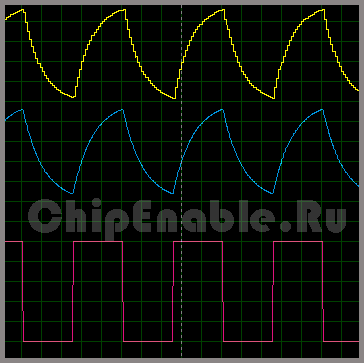
Результат моделирования программы в Proteus`e показан на рисунке ниже. Красный сигнал - это входной меандр частотой 200 Гц, синий - сигнал на выходе RC фильтра с постоянной времени 0.001 с, а желтый - сигнал обработанный микроконтроллером. Он имеет ступенчатую форму, так как после ЦАПа не подвергался фильтрации.
Как видно из рисунка форма сигнала микроконтроллера достаточно точно повторяет сигнал с выхода RC фильтра.
Заключение
Для наибольшего быстродействия коэффициент К лучше выбирать кратным степени 2 (например 2, 4, 8..), тогда компилятор будет заменять операцию деления сдвигами. В противном случае при высокой частоте дискретизации, микроконтроллер может не успевать рассчитывать следующее выходное значение фильтра. Я столкнулся с этим при моделировании.
Также необходимо учесть тот момент, что при больших значениях коэффициента К, переменная Dacc должна иметь достаточную разрядность, чтобы не наступало ее переполнение.

Comments
Если так, то зачем тогда менять аналоговый фильтр на цифровой, чтобы потом поставить аналоговый. Только из-за того, что для больших постоянных времени требуются большие значения R и C?
Заранее благодарен.
Я просто хотел узнать, каким образом можно будет сгладить неровности на выходе ЦАПа. Поставить RC-цепочку? Или каким-то другим способом?
А как на микроконтроллер е сделать ФВЧ?
Code:
Dout = (1-1/K)*Dout + 1/K;*Din;Dacc - лишняя переменная.
Причем, первое слагаемое имеет физический смысл заряда конденсатора, а второе - разряда. U(t)=U0*(1-e^(- t/T)), для нас t=1 (одна итерация). Таким образом обозначим K=e^(1/T), где T=R*C;
Для программного коэффициента К требуется согласование времен с АЦП, у Вас это хорошо описано.
Большое спасибо за отличную статью! Это как раз то, что мне нужно.
Скажите пожалуйста - как измениться программа для реализации полосового фильтра?
Правильно ли я понимаю : для полосового фильтра можно параллельно запустить в одном цикле два Ваших фильтра с разными постоянными времени и взять разницу результатов?
Очень давно я экспериментиров ал с аналоговой цветомузыкой. Результат был грустный.
Ваша статья повернула меня на цифровую тропу.
Спасибо !
RSS feed for comments to this post