AVR121: Повышение разрешения АЦП с помощью оверсемплинга ч1
23/12/2012 - 17:31
Pavel Bobkov
Микроконтроллеры AVR фирмы Atmel имеют в своем составе 10-ти разрядный аналого-цифровой преобразователь (АЦП). В большинстве случаев такой разрядности достаточно, но иногда возникают ситуации, когда требуется более высокая точность.
Существуют специальные методы обработки сигналов, позволяющие увеличить разрешение измерений. С помощью метода называемого “оверсемплинг и децимация” данная задача может быть решена без использования внешнего АЦП.
В этом руководстве рассмотрена теория и практическое применение данного метода.
Рассматриваемые вопросы:
- повышение разрешения с помощью оверсемплинга
- усреднение и децимация
- подавление шума с помощью усреднения
1 Введение
Микроконтроллеры AVR фирмы Atmel имеют в своем составе 10-ти разрядный аналого-цифровой преобразователь (АЦП). В большинстве случаев такой разрядности достаточно, но иногда возникают ситуации, когда требуется более высокая точность.
Существуют специальные методы обработки сигналов, позволяющие увеличить разрешение измерений. С помощью метода называемого “оверсемплинг и децимация” данная задача может быть решена без использования внешнего АЦП.
В этом руководстве рассмотрена теория и практическое применение данного метода.
Рисунок 1-1. Повышение разрешения
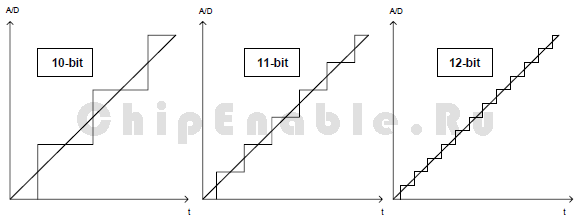
2 Теория работы
Перед чтением этого руководства мы бы рекомендовали вам ознакомиться с руководством «AVR120: Калибровка АЦП» и с разделом «АЦП» из технического описания на микроконтроллер AVR.
Изложенные ниже примеры и цифры рассчитаны для несимметричного входа в режиме непрерывного преобразования. Режим пониженного шума (ADC Noise Reduction Mode) не используется. Конечно, этот метод будет работать и в других режимах, но цифры для описанных примеров будут отличаться.
Опорное напряжение АЦП и его разрешение определяют шаг, с которым АЦП выполняет преобразование входного сигнала. У микроконтроллеров AVR в качестве опорного напряжения может выступать напряжение питания AVCC, внутреннее опорное напряжение 2.56 В/1.1 В или напряжение на выводе AREF.
Небольшое опорное напряжение обеспечивает высокую точность, но сужает динамический диапазон входного сигнала. Например, при опорном напряжении равном 2.56 В, точность результата преобразования будет приблизительно 2.5 мВ, а наибольшее входное напряжение, которое можно будет померить АЦП - 2.56В.
В качестве альтернативы можно было бы рассмотреть использование АЦП с секцией усиления. Это дает возможность измерять аналоговый сигнал с большей точностью, за счет динамического диапазона АЦП. Если это неприемлемо, то для улучшения разрешения АЦП можно использовать оверсемплинг. Хотя применение этого метода ограничивается характеристиками АЦП.
Важно понимать, что оверсемплинг и децимация уменьшают ошибки квантования АЦП, но не компенсирует его интегральную нелинейность.
2.1 Частота дискретизации
Теорема Найквиста-Шеннона гласит, что аналоговый сигнал, имеющий ограниченный спектр, может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, если частота выборки (дискретизации) превышает максимальную частоту спектра сигнала более чем в 2 раза. Минимальная требуемая частота дискретизации называется частотой Найквиста.
Формула 2-1. Частота Найквиста
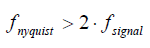
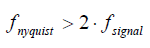
Где fsignal – это наивысшая частота входного сигнала.
Дискретизация сигнала с частотой выше частоты Найквиста называется оверсемплингом или дискретизацией с запасом по частоте. На практике обычно используют максимально возможную частоту дискретизации, чтобы получить как можно более точное представление измеряемого сигнала во временной области. Поэтому в большинстве случаев оцифрованный входной сигнал уже дискретизирован с запасом.
У микроконтроллеров AVR частота дискретизации АЦП определяется внутренней тактовой частотой и коэффициентом предделителя. Наименьший коэффициент дает наибольшую частоту дискретизации. Однако в определенный момент высокая тактовая частота АЦП будет уменьшать точность преобразования, то есть эффективное число разрядов (the Effective Number Of Bits ,ENOB) АЦП будет снижаться. Все АЦП имеют ограниченную полосу пропускания и АЦП микроконтроллеров AVR не исключение. Согласно техническому описанию, чтобы получить 10-ти разрядное разрешение, тактовая частота АЦП должна быть в диапазоне (50 – 200) кГц. Когда тактовая частота АЦП равна 200 кГц, частота дискретизации сигнала составляет ~ 15 kSPS (15 тысяч выборок в секунду), что ограничивает частоту входного сигнала до ~7.5 кГц. Тактовая частота АЦП микроконтроллеров AVR может иметь значение до 1 МГц, однако это будет снижать точность преобразований.
3 Теория
3.1 Оверсемплинг и децимация
Теория, стоящая за “Оверсемплингом и децимацией” достаточно сложная, но использование этого метода предельно простое. Нужно получить большее число выборок сигнала, увеличив частоту его дискретизации. Для каждого дополнительного бита разрешения требуется увеличение частоты дискретизации в 4 раза. Данное соотношение выражается формулой 3-1. Большее количество выборок нужно для лучшего представления входного аналогового сигнала при усреднении.
Формула 3-1. Частота оверсемплинга
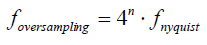
3.2 Шум
Чтобы этот метод работал правильно, интересующие нас сигнальные компоненты не должны меняться во время преобразования. Однако другой критерий для успешного повышения разрешения заключается в том, что выборки входного сигнала должны отличаться друг от друга. Это может выглядеть как противоречие, но в данном случае речь идет об изменении нескольких младших значащих разрядов (МЗР). Эти изменения следует рассматривать как шумовые составляющие сигнала. При дискретизации сигнала с запасом по частоте, он должен содержать шум, дающий небольшие вариации в сигнале. Ошибка квантования АЦП составляет, по крайней мере, 0.5 МЗР. Таким образом, шумовая амплитуда должна превышать 0.5 МЗР, чтобы «перебивать» его. Шум амплитудой 1-2 МЗР даже лучше, поскольку это будет гарантировать, что несколько выборок сигнала в итоге не будут иметь одинаковое значение.
При использовании данного метода шум должен иметь следующие характеристики:
- интересующие нас сигнальные компоненты не должны меняться значительно в течение преобразования,
- сигнал должен содержать шум,
- амплитуда шума должна быть не менее 1 МЗР.
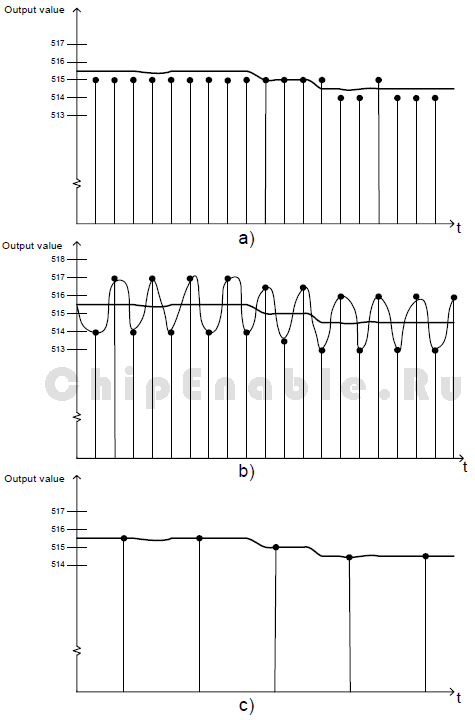
Обычно в сигнале присутствует некоторый шум во время преобразования. Это может быть тепловой шум, шум от ядра микроконтроллера, переключения портов ввода вывода, шум источника питания и так далее. В большинстве случаев этого шума будет достаточно для работоспособности рассматриваемого метода. В отдельных случаях потребуется добавить к входному сигналу некоторый искусственный шум. Этот метод известен как дизеринг. Рисунок 3-1 (а) показывает проблемы измерения сигнала, значение которого находится между двумя шагами квантования. Усреднение четырех выборок сигнала не помогло бы, поскольку у результата будет такое же низкое значение. Это может только ослабить флуктуации сигнала. Рисунок 3-1 (b) показывает, что добавляя к сигналу искусственный шум, младшие значащие разряды результата преобразования будут переключаться. Сложение четырех выборок этого сигнала уменьшает шаги квантования вдвое, что дает лучшее представление входного сигнала, как показано на рисунке 3-1 (c). “Виртуальное разрешение” АЦП увеличится с 10-ти до 11-ти. Этот метод известен как децимация и будет объяснен дальше в разделе 3-3.
Рисунок 3-1. Увеличение разрешения с 10-ти до 11-ти бит
Другой причиной использования этого метода является увеличение отношения сигнал-шум. Повышение эффективного числа разрядов (ENOB) распространит шум по большему двоичному числу, поэтому влияние шумов на каждый двоичный разряд будет снижаться. Удвоение частоты дискретизации позволяет снизить шум в полосе частот на 3 дБ и увеличить точность измерений на 0.5 бита.
3.3 Усреднение
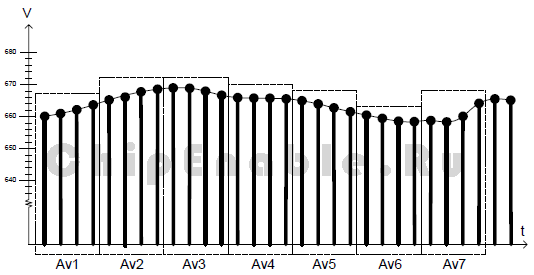
Обычный смысл усреднения заключается в сложении m выборок сигнала и делении полученного результата на m. Это так называемое нормальное усреднение. Усреднение данных, полученных с АЦП, эквивалентно низкочастотному фильтру и позволяет ослабить флуктуации сигнала или шум, и сгладить пики входного сигнала. Очень часто для этого также используется метод скользящего среднего. Он заключается в усреднении выборок сигнала внутри циклической очереди. В этом случае каждая усредненная выборка сигнала будет представлена несколькими самыми последними выборками. Что будет давать небольшую временную задержку. Усреднение этим методом может быть сделано с или без перекрытия окон. Рисунок 3-2 показывает семь (Av1 – Av7) независимых результатов скользящего среднего без перекрытия.
Рисунок 3-2. Принцип усредняющего среднего
Важно помнить, что нормальное усреднение не увеличивает разрешение преобразования. Децимация и интерполяция представляют собой усредняющие методы, которые в сочетании с оверсемлингом увеличивают разрешение. Интерполяцией в цифровой обработке сигналов называют метод, основанный на оверсемплинге и низкочастотной фильтрации. В этом смысле интерполяция используется для получения новых промежуточных выборок сигнала путем усреднения большого количества выборок. Дополнительные выборки m, полученные с помощью оверсемплинга сигнала, складываются также как при нормальном усреднении, но результат не делится на m. Вместо этого он сдвигается вправо на n, где n – количество дополнительных битов разрешения. Однократный сдвиг двоичного числа вправо эквивалентен делению на 2. Как видно из формулы 3-1 повышение разрешения с 10 до 12 бит требует суммирования 16-ти 10-ти разрядных значений. Результат этой суммы будет 14-ти разрядным, где последние два бита не содержат ценной информации. Чтобы вернуться обратно к 12-ти битам, нужно масштабировать результат. Масштабирующий коэффициент sf, определяемый формулой 3-2, это коэффициент на который нужно делить сумму из 4^n выборок для получения правильного результата. Где n – требуемое количество дополнительных разрядов разрешения.
Формула 3-2
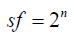
3.4 В каких случаях “Оверсемплинг и децимация” будут работать?
Обычно сигнал содержит некоторый шум. Этот шум, часто имеющий характеристику Гауссовского шума, более известен как белый шум или тепловой. Он отличается широкой полосой частот и равномерным распределением энергии по всей полосе. В этих случаях метод “оверсемплинга и децимации” будет работать, если амплитуда шума достаточна для переключения МЗР преобразования АЦП.
В других случаях может понадобиться добавить к входному сигналу искусственный шум. Этот метод называют дизерингом. Форма этого шума должна соответствовать Гауссовскому шуму, но сигнал периодической формы тоже будет работать. Какой частоты должен быть этот шумовой сигнал, зависит от частоты дискретизации. Эмпирическое правило гласит: “При сложении m выборок, период шумового сигнала не должен превышать периода m выборок”. Амплитуда шума должна быть не менее 1 МЗР. При сложении искусственного шума с входным сигналом важно помнить, что среднее значение шума равно нулю; недостаточно высокий оверсемплинг (недостаточный запас по частоте дискретизации) может вызвать смещение, как показано на рисунке 3-3.
Рисунок 3-3. Смещения, вызванные недостаточной частотой дискретизации
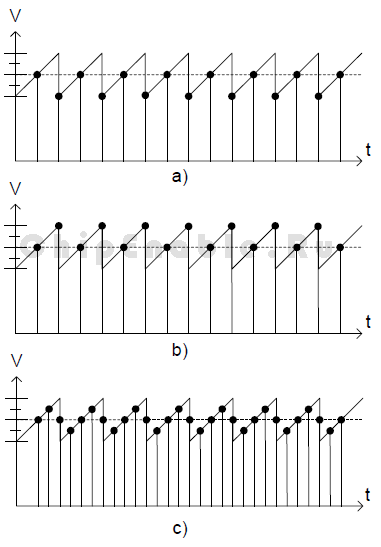
Пунктирная линия иллюстрирует среднее значение пилообразного сигнала. Рисунок 3-3 (а) представляет случай отрицательного смещения. На рисунке 3-3 (b) показан случай положительного смещения. И на рисунке 3-3 (с) частота дискретизации выбрана подходящей и смещения нет. Чтобы создать искусственный шум, можно использовать один из счетчиков микроконтроллеров AVR. Так как счетчик и АЦП используют один и тот же источник тактового сигнала, это позволяет синхронизировать шум и частоту дискретизации, чтобы избежать смещения.

Comments
патриотично)
Наверно потому что Найквист эту теорему не предлогал и не доказывал. А соответственно теорема была предложена и доказана Котельниковым.
Минимальный уровень - это шум, максимальный - опорное напряжение. Уменьшаем опору - соотношение меняется. Я понимаю это так.
С другой стороны шум всегда есть, и уменьшение уровня опоры, конечно, ведет к уменьшению этого соотношения, но тогда АЦП тут почти ни при чем.
Впрочем, наверно, так и есть как вы сказали.
RSS feed for comments to this post