3.5 Пример1

   Пивовар из Дублина хочет измерять температуру процесса на своем пивоваренном заводе. Номинальное напряжение соответствующее его окружающей температуре - 2.5 В. Рисунок 3-4 показывает характеристику устройства измерения температуры.

Рисунок 3-4. Функция напряжение/температура

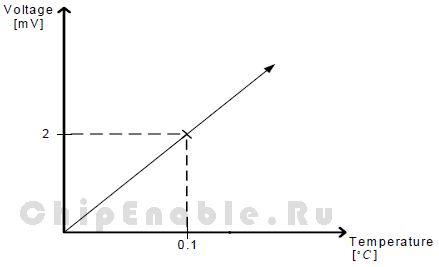
   Пивовар не хочет уменьшать динамический диапазон входного сигнала и выбирает величину опорного напряжения АЦП – 5 В. В этом случае 10-ти разрядный АЦП не может обеспечить требуемой точности, поскольку шаг квантования будет составлять ~5 мВ, что соответствует температурному разрешению 0.25°C. Пивовар хочет, чтобы результат имел точность 0.1 °C, а это требует проведения измерений с разрешением меньше 2 мВ. Если бы измерения были выполнены 12-ти разрядным АЦП, шаг измерения напряжения составил бы ~1.22 мВ. Пивовару нужно трансформировать 10-ти разрядный АЦП к виртуальному 12-ти разрядному. Поскольку входной сигнал меняется очень медленно, высокая частота дискретизации не требуется. Согласно техническому описанию AVR для обеспечения эффективного 10-ти разрядного разрешения тактовая частота АЦП должна быть в диапазоне от 50 кГц до 200 кГц. По этой причине пивовар выбрал тактовую частоту АЦП 50 кГц. Это соответствует частоте дискретизации ~3800 SPS (выборок в секунду). Допустим, в какой-то момент значение напряжения, представляющее температуру, составляет 2.4729V. Таблица 3-1 показывает варианты измерений этого значения с различным разрешением при Vin = 2.4729V и VREF = 5V.

Таблица 3-1. Варианты разрешения

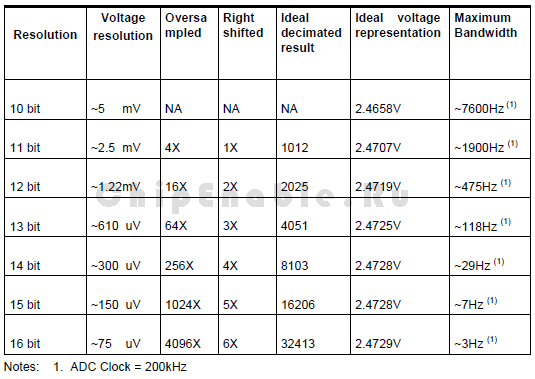
  Допустим, в результате одиночного преобразования было получено значение 505, на первый взгляд оно может выглядеть правильным. Но это число также соответствует, напряжению 2.4658 В. Это ставит пользователя в неопределенность и вызывает ошибки в температурных измерениях, что в некоторых случаях может быть неприемлемо. Как было замечено раньше, сигнал обычно содержит некоторый шум, позволяющий использовать метод децимации.

   Чтобы увеличить разрешение на один бит, складываем ближайшие 4 выборки. Поскольку выборки содержат шум, они отличаются друг от друга несколькими младшими значащими разрядами. Например, сложили такие четыре выборки: 508 + 507 + 505 + 505 = 2025. Согласно принципу децимации полученную сумму нужно масштабировать к 11 разрядному числу. Для этого нужно сдвинуть результат вправо n раз, где n – количество желаемых дополнительных битов разрядности. Результат – 1012. После увеличения разрешения, можно неожиданно получить выборки между исходными шагами квантования. Тем не менее, сигнал оцифрован с достаточным запасом по частоте, чтобы увеличить разрешение дальше до 12 бит. Сложив 16 10-ти разрядных выборок и сдвинув результат вправо на 2 разряда, мы это сделаем. Результат – 2025. Это более достоверное число, потому что, при использовании 12-ти разрядного результата, погрешность снижается до ~1.22 мВ. Этот пример показывает, что пользователь, начав измерять медленно меняющийся сигнал с частотой дискретизации 3800 выборок в секунду и точностью ~5мВ, теперь имеет 240 выборок с 12-ти битным разрешением и точностью ~1.22 мВ. 

   Также пользователь может хотеть выровнять флуктуации сигнала путем усреднения 16-ти 12-ти разрядных выборок. Для этого складываются 16 выборок и результат делиться на 16. В итоге пользователь имеет 15 выборок в секунду, каждая из которых состоит из 16 усредненных 12-ти разрядных соседних выборок (15 * 16 * 16 = 3840)

- “оверсемплинг и децимация” будут использовать шум для повышения разрешения,
- нормальное усреднение будет уменьшать последствия случайного шума.

3.6 Пример 2

   Следующий пример покажет, что для достижения высокой точности нет необходимости использовать внешний АЦП. Здесь используется генератор сигналов для формирования линейного нарастающего сигнала от 0 В до 5 В. В малошумящем приложении с генератором сигналов и AVR микроконтроллером, размещенном на отладочной плате STK500, может не оказаться шума, достаточного для переключения нескольких младших разрядов 10-ти битного сигнала. В этом случае к входному сигналу необходимо добавить искусственный шум. Для этих целей могут быть использованы 4 метода:

- добавление шума, создаваемого генератором сигналов, непосредственно к входному сигналу,
- генерация шума с помощью AVR, используя ШИМ, и добавление его к входному сигналу,
- добавление шума, создаваемого AVR, на вход AREF, когда в качестве опорного напряжения VREF используется напряжение на выводе AVCC,
- добавление шума, создаваемого AVR, на вход AREF, когда в качестве опорного напряжения VREF используется источник, подключенный к AREF.

   Простейший способ “загрязнить” сигнал – добавить белый шум непосредственно к нему. Однако в большинстве случаев у пользователя нет или он не хочет иметь подобные шумовые сигналы в измерительных приложениях. Более доступный метод состоит в том, чтобы установить один из счетчиков AVR в режим формирования ШИМ сигнала и пропустить этот “шум” через низкочастотный фильтр, чтобы представить его постоянным сигналом с пульсациями в несколько МЗР. Пример подобного фильтра показан на рисунке 3-5.

Рисунок 3-5. Низкочастотный фильтр

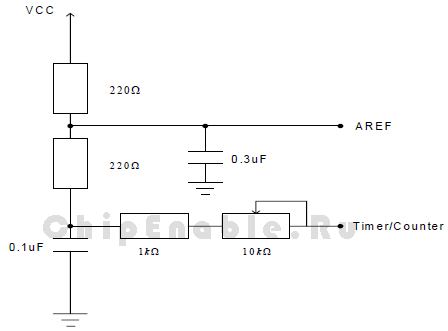
   Если VCC = 5 В, отфильтрованный сигнал на выводе AREF представляется уровнем 2.5 В, когда рабочий цикл счетчика 0% и 5 В, когда рабочий цикл 100%. В этом примере рабочий цикл ШИМ сигнала – 50%, а базовая частота ~ 3900 Гц. Потенциометр величиной 10 кОм используется, чтобы регулировать пульсации. ШИМ сигнал используется или в качестве опорного напряжения АЦП, или в качестве шумового генератора, подключенного к выводу AREF. AVCC при этом установлен в качестве опорного напряжения АЦП. Идея состоит в том, что небольшие вариации опорного напряжения будут давать такой же эффект, как и небольшие изменения входного сигнала, при этом, совершенно не затрагивая его.

   Измерение линейно нарастающего сигнала представлено на рисунках 3-7, 3-8, 3-9, 3-10. Рисунок 3-7 показывает 10-ти разрядное дискретное представление входного сигнала, полученное без добавления искусственного шума. Здесь очень явно видны шаги квантования. Чтобы улучшить разрешение сигнала, необходимо уменьшить их.

   Рисунок 3-8 показывает 12-ти разрядное дискретное представление входного сигнала, когда AREF используется в качестве опорного напряжения АЦП и добавлено несколько разрядов шума. Согласно формуле 3-1, каждый 12-ти разрядный результат состоит из 16-ти 10-ти разрядных выборок. Рисунок 3-9 показывает 14-ти разрядное дискретное представление входного сигнала, а рисунок 3-10 16-ти разрядное. Когда измеряется сигнал содержащий шум, или когда опорное напряжение варьируется как в этом примере, важно помнить, верхнее и нижнее значения уменьшаются на величину амплитуды шумового сигнала, что дает небольшое снижение динамического диапазона.

Рисунок 3-6. Входной сигнал, 0 – 5 В

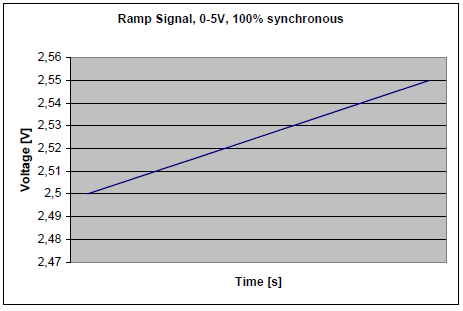
Рисунок 3-7. Нарастающий сигнал, представленный с 10-ти разрядным разрешением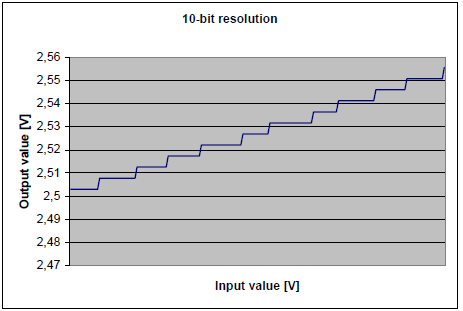


Рисунок 3-8. Нарастающий сигнал, представленный с 12-ти разрядным разрешением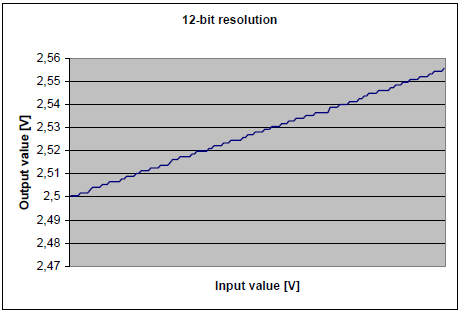


Рисунок 3-9. Нарастающий сигнал, представленный с 14-ти разрядным разрешением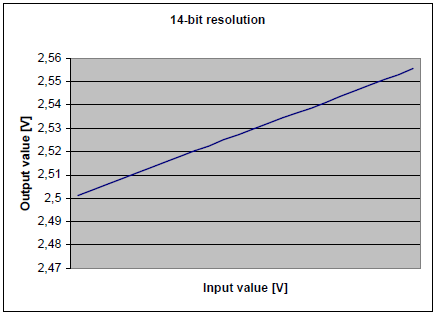


Рисунок 3-10. Нарастающий сигнал, представленный с 16-ти разрядным разрешением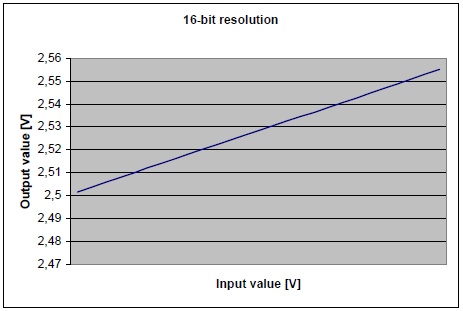

 
    Легко видеть, что, используя метод оверсемплинга и децимации, можно значительно увеличить разрешение сигнала.

Резюме

   Когда АЦП делает выборки сигнала, он кодирует его дискретными шагами. Это вносит некоторую ошибку, известную как ошибка квантования. Использование нормального усреднения будет только сглаживать флуктуации сигнала, тогда как метод оверсемплинга и децимации будет увеличивать разрешение. Суть метода заключается в дискретизации сигнала с более высокой частотой и вычислении новой выборки сигнала на основе полученных дополнительных выборок. Требуемая частота дискретизации может быть найдена по формуле 3-1. Сложение дополнительных выборок и сдвиг результата вправо на n, будет давать результат с разрешением, увеличенным на n разрядов. Усреднение четырех результатов преобразования дает новый результат, как если бы АЦП дискретизировал сигнал с частотой в одну четверть, но это также дает эффект усреднения шума квантования, улучшая отношение сигнал-шум. Что увеличивает количество эффективных разрядов АЦП и уменьшает ошибку квантования. Доступность скоростных АЦП и низкая стоимость памяти, делает применение метода оверсемплинга и децимации экономически целесообразным.

Подведем итоги:

- в сигнале должен присутствовать шум амплитудой не меньше 1 МЗР
- если амплитуда шума недостаточна, добавьте шум к сигналу
- накапливайте 4*n выборок, где n – количество дополнительных битов разрешения
- масштабируйте аккумулированный результат, путем его сдвига вправо на n разрядов
- скомпенсируйте ошибки в соответствии с руководством AVR120

Ссылки

AVR121:Повышение разрешения АЦП с помощью оверсемплинга. Ч1
AVR121:Enhancing ADC resolution by oversampling

AVR120:Characterization and Calibration of the ADC on an AVR