При программировании микроконтроллеров разработчики иногда сталкиваются с проблемой вычисления квадратного корня. Например, данная операция требуется при выполнении быстрого преобразования Фурье или вычислении среднеквадратического значения сигнала.
В стандартной библиотеке Си – math.h, есть функция для вычисления квадратного корня sqrt(), которой при желании можно воспользоваться. Она работает с числами типа float, обеспечивает высокую точность результата, но требует для своей работы длительного времени. Для микроконтроллера AVR это порядка 3000 циклов тактовой частоты (проверено в компиляторе IAR на разных уровнях оптимизации).
Если к точности вычисления корня не предъявляются высокие требования, можно воспользоваться упрощенным алгоритмом, занимающим меньше места в памяти и выполняющим вычисления в несколько раз быстрее.
Алгоритм выглядит так.
{
unsigned int root(unsigned int x)
unsigned int a,b;
b = x;
a = x = 0x3f;
x = b/x;
a = x = (x+a)>>1;
x = b/x;
a = x = (x+a)>>1;
x = b/x;
x = (x+a)>>1;
return(x);
}
Как мне подсказали умные люди, алгоритм основан на итерационной формуле Герона.
Xn+1 = (A/Xn + Xn)*1/2
где А – фиксированное положительное число, а X1 – любое положительное число.
Итерационная формула задаёт убывающую (начиная со 2-го элемента) последовательность, которая при любом выборе X1 быстро сходится к квадратному корню из числа А.
Ради интереса я переписал алгоритм в явном виде. Скомпилированный, он ничуть не потерял ни в быстродействии, ни в объеме. Объем даже на пару байтов уменьшился.
unsigned int root1(unsigned int a)
{
unsigned int x;
x = (a/0x3f + 0x3f)>>1;
x = (a/x + x)>>1;
x = (a/x + x)>>1;
return(x);
}
Недостатки приведенного кода в том, что он работает только с целыми 16-ти разрядными числами и при больших значениях аргумента вычисления становятся не точными. Правда, точность вычислений можно повысить, добавив еще несколько итераций, но за это естественно придется платить быстродействием.
Код занимает прядка 70 байт и выполняется ~ за 700 циклов. Данные получены в компиляторе IAR AVR при medium оптимизация по скорости.
Точность вычисления данного алгоритма можно оценить по приведенному ниже графику. Синий график построен по значениям, полученным c помощью библиотечной функции sqrt(), красный график по значениям функции root().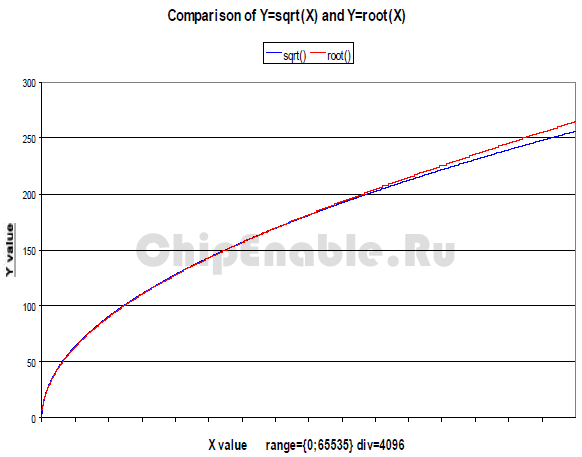
В ходе обсуждения моей заметки, те же самые умные люди подсказали еще один алгоритм вычисления квадратного корня.
unsigned int isqrt(unsigned int x)
{
unsigned int m, y, b;
m = 0x4000;
y = 0;
while (m != 0){
b = y | m;
y = y >> 1;
if (x >= b) {
x = x - b;
y = y | m;
}
m = m >> 2;
}
return y;
}
~50 байт, <200 циклов для IAR AVR с medium оптимизацией по скорости. Точность не оценивал.

Comments
x = b/x;
a = x = (x+a)>>1;
Но для AVR, данный алгоритм не оптимальный, т.к. деление выполняется долго. Посмотрите на метод бинарного поиска целочисленного квадратного корня (только умножение и сложение), описан в книге "Алгебраические трюки для программиста". Там ещё описан алгоритм без умножения, только сдвиги, сложения и битовые операции. Можно попробовать адаптировать для AVR его, тогда выигрыш во времени будет значительный.
Xn+1 = (Xn + A/Xn)*1/2
A - число из которого требуется вычислить корень, X1 - любое положительное число.
Code:
unsigned int root(unsigned int a)
{
unsigned int x;
x = (a/0x3f + 0x3f)>>1;
x = (a/x + x)>>1;
x = (a/x + x)>>1;
return(x);
}
получаются точно такие же результаты. Как по ответам, так и по скорости исполнения кода. А по объему даже небольшой выигрыш. Зачем надо было так мудрить?
подскажите пожалуйста как проделать это с переменной типа long?
Для скорости выполнения. ставим брейкпойнт перед вызовом функции и после,запускаем симуляцию - обнуляем cycle counter,запуска ем симуляцию - и новое значение будеть скоростью выполнения (также можно увидеть сколько время исполняеться функция в мкс или мс).
Затем запускаешь компиляцию проекта и с левой стороны (в окне отображения структуры проекта) ищешь файлы с расширением *.lst Они будут созданы для каждого программного модуля. В конце этого файла есть табличка со списком функций и значениями занимаемой памяти.
Чтобы прикинуть скорость выполнения какого-нибудь куска кода (обычно функции), я прогоняю этот код в программном симуляторе IAR`a. Включаю опцию Project > Options > Linker > Debug Information ... Запускаю компиляцию и отладку с помощью кнопки Debug (Ctrl+D). Устанавливаю брейкпоинты, открываю окно с регистрами микроконтроллер а (меню View > Register) и запускаю код на выполнение по шагам (F11) или непрерывно (f5). В окне регистров в разделе CPU Register есть строка CYCLES. Она отображает число прошедших тактов. По показаниям этого числа можно прикинуть сколько тактов занимает выполнение функции.
То же самое можно делать и в AVR Studio. Там это даже лучше получается, потому что студия моделирует прерывания, а IAR нет.
Можете проверить функцию:
Code:
unsigned int isqrt(unsigned int x)
{
unsigned int m, y, b;
m = 0x4000;
y = 0;
while (m != 0)
{
b = y | m;
y = y >> 1;
if (x >= b)
{
x = x - b;
y = y | m;
}
m = m >> 2;
}
return y;
}
Сколько занимает и как долго выполняется?
F = 8 MHz, ATmega8, optimization O0 (none):
размер 14 байт.
скорость 540 циклов - 67.5uS
F = 8 MHz, ATmega8, optimization Os (none):
размер 14 байт.
скорость 2 циклf - 0.25uS
#include
unsigned int value = 0;
unsigned int isqrt(unsigned int x)
{
unsigned int m, y, b;
m = 0x4000;
y = 0;
while (m != 0)
{
b = y | m;
y = y >> 1;
if (x >= b)
{
x = x - b;
y = y | m;
}
m = m >> 2;
}
return y;
}
int main(void)
{
asm("nop");
value = isqrt(4096);
asm("nop");
while(1);
}
подскажите пожалуйста как проделать это с переменной типа long?
unsigned long isqrt(unsigned long x)
{
unsigned long m, y, b;
m = 0x4000;
y = 0;
while (m != 0)
{
b = y | m;
y = y >> 1;
if (x >= b)
{
x = x - b;
y = y | m;
}
m = m >> 2;
}
return y;
}
1) 49 - 1 = 48
2) 48 - 3 = 45
3) 45 - 5 = 40
4) 40 - 7 = 33
5) 33 - 9 = 24
6) 24 - 11 = 13
7) 13 - 13 = 0
7 циклов, корень числа 49 - 7.
И кстати при работе с МК типа AVR-ки лучше избегать делений, т.к. у AVR ядра нет аппаратного деления, а программное занимает дофига тактов. Другое дело ARM Cortex-M3 и выше, у которых деление выполняется за 2... 12 тактов.
sqrt(a*2^16)=2^ 8*sqrt(a).
Удобно в качестве такого отрезка взять значения [2^30-2^31), потому что остальные значения можно свести к нему побитовым сдвигом и при этом не будет происходить потеря точности. Сначала вычисляем первый значащий бит (программно половинным делением или процессорной инструкцией, например на ARM это __clz). Потом сдвигаем входное число на это кличество бит и вычисляем корень, полученное значение сдвигаем обратно на в два раза меньшее количество).
Для вычисления корня на отрезке интерполируем его многочленом Лагранжа (параболой). Например, возьмем в качестве точек многочлена 2^30, 1,5 * 2^30, 2^31. Можно воспользоваться сторонним сервисом, и не возиться с вычислением коэффициентов. У меня получилась такая формула:
-x^2/499100218444523 + x/52370 + 14575
Очевидно, напрямую её использовать нельзя, потому что значения не влазят даже в диапазон целых. Но надо учесть, что нам важны только 16 бит результата, поэтому можно немного схитрить и вынести что-то за скобки.
(-x/9530269590 + 1) * x/52370 + 14575
(-x/145420 + 65536) * (x/65536) / 52370 + 14575
Ну и последнее - заменить деление на умножение. Допустим, у нас в резерве 30 бит числа. Мы хотим поделить некое число x, например, на 543. Вычисляем, в числе 543 есть 10 бит, в х 16 бит.
x / 543 * 2^26 / 2^26
x * (2^26 / 543) / 2^26
x * 123589 / 2^26
Теперь эти знания применяем к своему многочлену.
(-x/2^14 * 7384 / 2^16 + 2^16) * (x/2^16) / 2^16 * 20503 / 2^14 + 14575
Не ручаюсь за правильность коэффициентов, надо внимательно проверить.
Когда писал, не учел одну штуку, число бит может быть нечетным, отрезок надо брать больше.
Естественно, алгоритм будет быстро работать при наличии аппаратного умножения.
Code:
m = 0x4000;?Это половина от максимума int ?
А вот 2й вариант работает отлично, спасибо!
Мне нужно считать корни из больших чисел до 250 000 000, поэтому увеличил количество:
Code:
x = (a/x + x)>>1;до 7 и точность приемлима.
RSS feed for comments to this post